BeatGraphs

Breaking it down

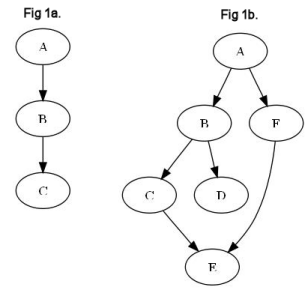
To explain how BeatGraphs work, it is easiest to start with the smallest unit, a BeatWin. When any team defeats another team they are awarded a BeatWin to that team. BeatWins are represented by the notation A→B where A has a BeatWin over B. A BeatPath is considered any chain of BeatWins that can lead from one team to another. For example, if A→B, A has a BeatPath to B from that direct win. If then B→C, B has a BeatPath to C, and therefore there is a BeatPath A→B→C which is to say A has a BeatPath to C through B (see Fig 1a). Through transitive logic we assume that since A has proven themselves better than B (A→B), and B has proven better than C (B→C), A is therefore better than C.

By using BeatPaths we essentially can say, "Since team A has defeated team B who defeated C, A should have the highest ranking and C the lowest." With a slightly more complex graph sometimes there are teams with no relation to each other, but based on the relationships they do have, we try to be as specific as we can. In the next example (see Fig 1b) we have several BeatPaths we are familiar with. We know that A is the best because they have a BeatPath to every other team. Teams that do not have paths to each other have an ambiguous relationship. While both C and D lost to B, it cannot be determined which is better between the two. Additionally, even though the graph shows D above E, because there is no direct relation between the two it cannot be explicitly proven that either team is better than the other. These problems will be addressed later when we discuss rankings.

Making a BeatLoop

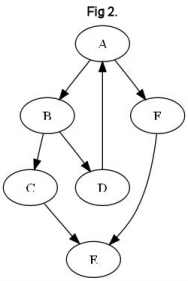
Quite frequently through the season there will be results which contradict preexisting relationships on the graph. When team D defeats team A which already had a BeatPath to D, a BeatLoop is created A→B→D→A (see Fig 2). This causes an arrow to point up in the graph, and prevents us from using this hierarchy to establish relationships between the teams. When BeatLoops occur, they must be resolved in order to return to a graph which represents all of the unambiguous information that we have regarding the teams. This is where the majority of the work and debate is done. To see how BeatPaths are broken, continue to the next section.